Dodecaphonic Pre-Compositional Process

Developing a Dodecaphonic Row. The central concept behind dodecaphony is the notion that all of the music should arise from a single compositional element: the 12-tone row. A tone row (or series), as prescribed by Schönberg, must contain each of the twelve chromatic pitches (called a pitch class) once and only once. This avoidance of repetition is construed so that there is no sense that any pitch has more weight than another (to contrast with the major/minor key system wherein there exists a clear hierarchy within the relationships between pitches, such as the tonic, dominant, mediant, etc.). Rather than using the term atonal, which can have a negative connotation, Schönberg employed the term pantonal to describe the listening experience (which is also often referred to as non-tonal).

The tone row is the initial point of departure for the composer, and as such can be created simply from a melodic idea. However, many composers choose to construct a row from an abstract interval-based concept before composing, in the true sense, begins. To intensify the tightly knit approach of using a tone-row, the series can be broken down into interrelated groups containing similar constructs within themselves. For instance, two groups of six notes (called hexachords) or three groups of four notes (called tetrachords) can be arranged as long as there is no repetition of pitches between the groups.

For our purposes, we will create a series from two hexachords. Note that we have carefully devised a sequence of intervals within the first hexachord (m3, M2, m2, tritone, m2) that is duplicated in the second (despite some directional differences). The two hexachords are additionally related by the tritone (C-F#) – an interval regarded by some composers as an axis of non-tonal music similar to the tonic/dominant relationship of tonal practices.

There are many varied approaches to creating tone rows based on an abstract pre-compositional idea, such as series that contain all intervals, others that have some extra-musical significance (based on letters of names, etc.), or those that actually have tonal implications (such as triadic construction or scalar material). Each composer should develop their rows based on the expressive needs of the piece at hand; it is a more flexible system than many practitioners and those in the Academy admit.

Dodecaphonic Inversions. The next essential 12-tone principle maintains the idea that any piece of musical material can be articulated in its original version (referred to henceforth as its prime) as well as its inversion wherein the direction of each interval is reversed (e.g. an ascending minor third in the prime will become a descending minor third in the inversion). To derive the inversion of a row, we can create a chart (here based on the first note of the row we have created). Based on the illustrated below, the inversion of our prime row would read: C, Eb, F, E, Bb, B, F#, A, G, G#, D, C#.

The Four Basic Forms. In addition to the prime and inversion forms, each row can be articulated from last pitch to first, a transformation called retrograde. As applied to the inversion form of the row, this is called retrograde-inversion. As such, the rows notated below illustrate the four basic forms of our original series. Note that we have added an accidental before each note, regardless if it seems to need a natural or not. This stems from Schönberg’s practice to avoid any ambivalence in the total-chromatic field.

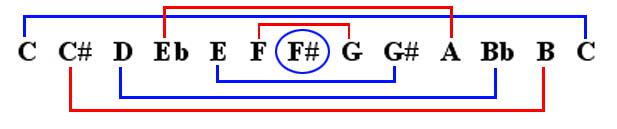
Also, it is important for the student to realize that without any tonal hierarchy, there exists no functional difference between, say, C# and Db or G# and Ab. The preference between the two will depend on the situation in the actual composition and what is clearest for the performer to read. With this in mind, some theorists substitute numbers 0-11 for the pitch names. Although this is useful for analytical purposes, for our compositional needs we will preserve the traditional note names.

The Dodecaphonic Matrix. As we have observed, dodecaphony inherits an important premise from the Renaissance composers’ ideal to create with an economy of means in order to provide a unified and organic artistic expression, or more simply put, as much musical development possible from as little primary material possible. As such, Schönberg devised a visual way for the composer to examine all possible versions of a given row by borrowing an idea from mathematics: the matrix. This should by no means be interpreted that 12-tone music is somehow inordinately ‘mathematical’, just as artists outlining horizon lines to organize perspective in a painting should as well not be so accused.

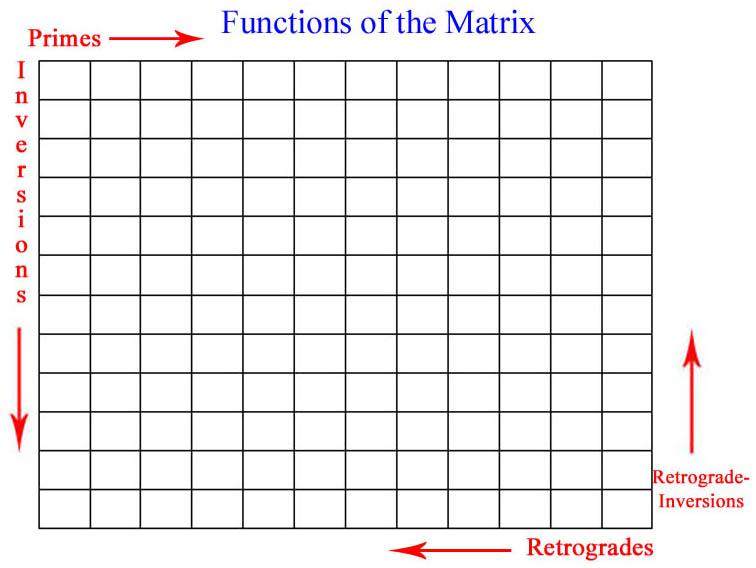
Extrapolating a Matrix from a Row: Inversions. After inserting our original prime series as the first row in the matrix, reading from left to right; the inversion of this row can be inserted reading down in the first column.

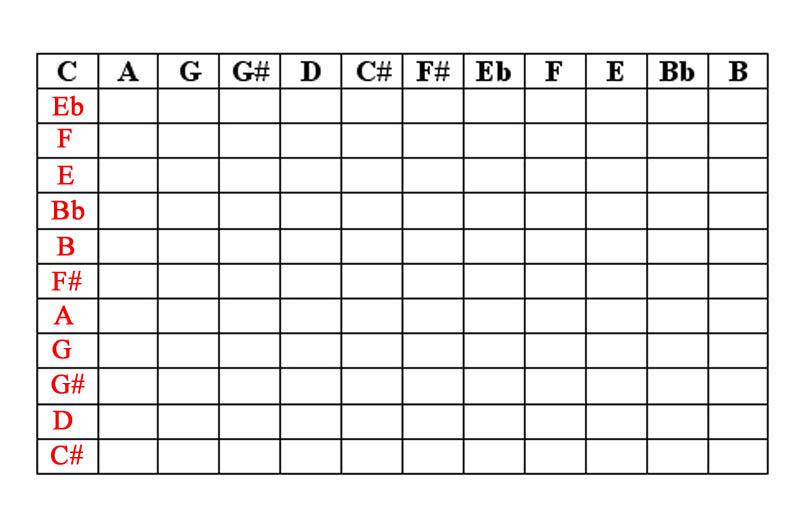
Extrapolating a Matrix from a Row: Transpositions. The final step to creating our matrix is the simple task of deriving the transpositions.

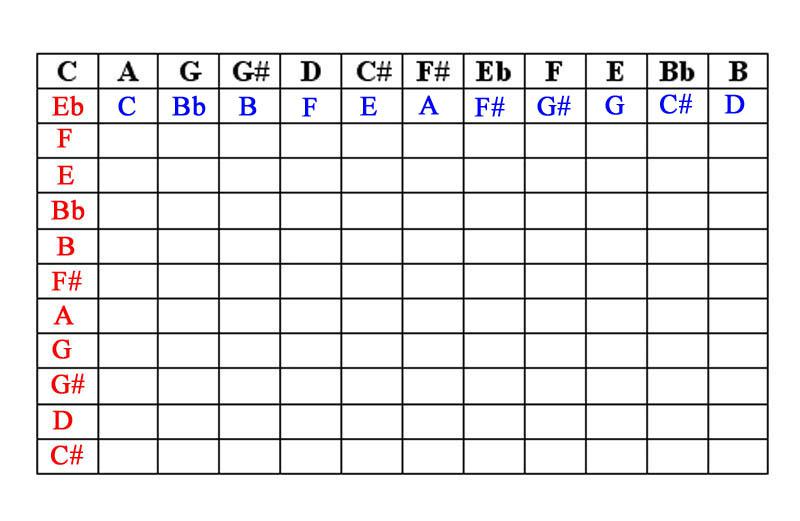
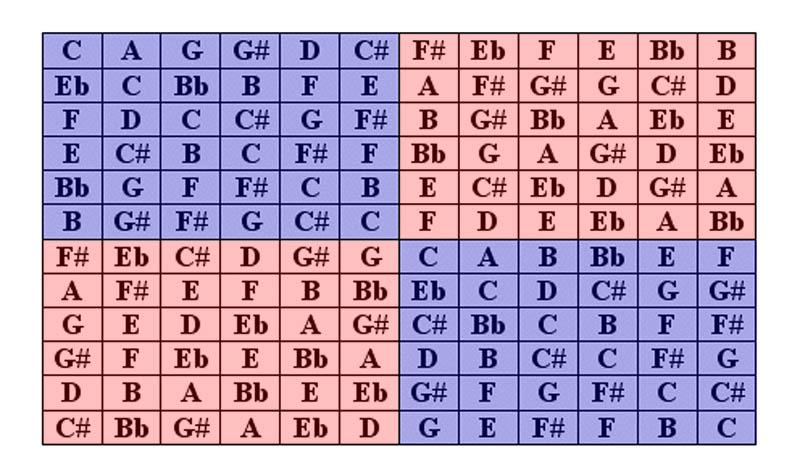
Complete Matrix. The final version of our matrix will feature all of the forty-eight transformations (four basic forms, twelve transpositions each) that can be derived from the original row. To make viewing easier, we have used contrasting colors to clearly distinguish adjoining hexachords.

B. Lyrical Dodecaphonic Piece

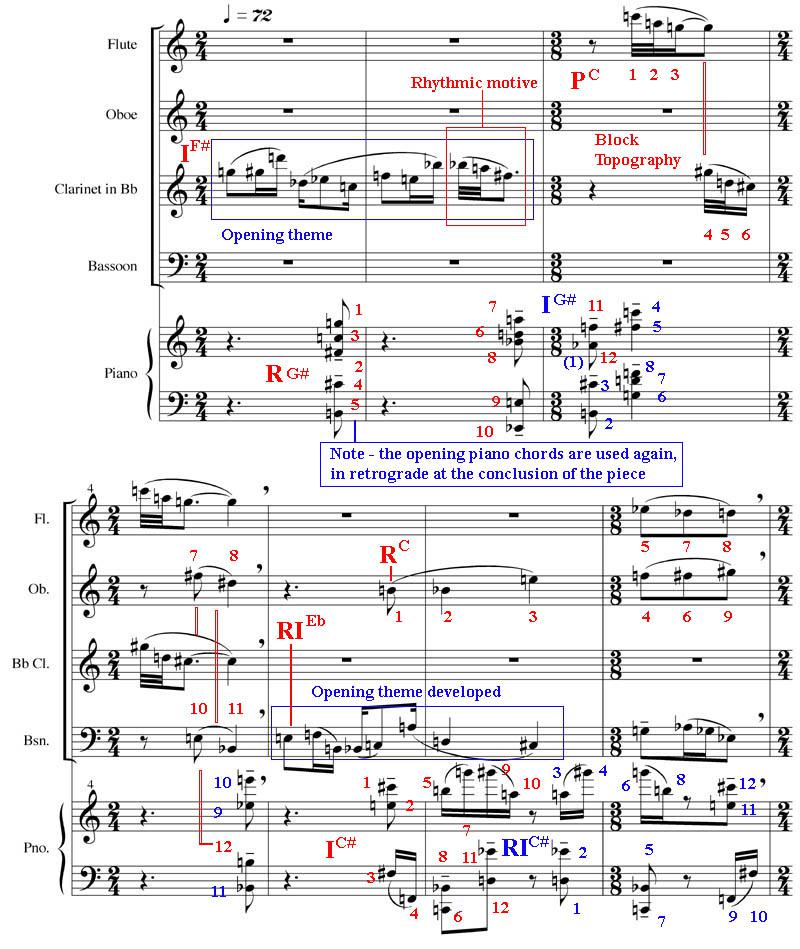
Composing with a 12-Tone Row. Although some composers have developed extremely complex methods of using a matrix, two fundamental methods will be explored in depth here. Theorists have adopted certain cartography terminology, such as ‘topography’, perhaps because deciphering the contoured layout of a 12-tone composition can be akin to finding one’s way about an unfamiliar landscape by using a standard map. There are two essential types of topography: block and polyphonic.

Block topography involves all musical materials being derived from one row at a time, regardless of the number of voices or whether the music is homophonic or contrapuntal. Polyphonic topography, on the other hand, allows each voice (or voice groups) to develop from individual row transformations. Some compositions apply only one topography type, while others combine both approaches. In our sample pieces, we will explore primarily one over the other (per work) without creating too many self-imposed limitations.

Regarding analysis, rows will be labeled based on their transformation type [P (prime), I (inversion), R (retrograde), RI (retrograde-inversion)] and transposition. Transpositions are named based on the first pitch of the row if the row form is prime or inversion. Retrogrades and retrograde-inversions are labeled in terms of the prime and inversion rows from they are derived. Arabic numbers (1-12) are used to indicate what pitch in a specific transformation is being articulated.

Lyric Composition. This piece will employ mostly block topography in a ternary form structure. The slurs are used to clearly highlight the melodic voice as it weaves its way through the texture. Although block topography can be used in a strictly chronological progression through each series (applying pitches 1 to 12 in order), we can also articulate each hexachord in tandem (especially since the particular row at hand was constructed from a hexachordal perspective). As well, reiterated patterns within the course of the series allow for some repetition. This is exploited both in the opening section repeated chords and the brief ostinati that characterize the central section.

We begin with our initially conceived row at the outset of the composition, but henceforth allow for some freedom regarding what row to employ. However, our choices are not simply capricious ones: shared tones are an interesting and seamless method of ‘modulating’ from one row to the next (for example, the final two pitches in bar 11, A and C, are the first two pitches of the next transformation). In bar 5 we will note that although only one row is used, it is employed simultaneously in its prime and retrograde forms, thus lying somewhere between block and polyphonic topographies.

Also note that a slight alteration to the precise order are made in bar 3: here the melodic contour made better sense to have the F# after the A rather than before. Schönberg himself admitted to making these kinds of alterations when the expressive needs of the music required them. Once again, the student will observe that structures and systems provide a means with which to establish a working method, but should never inhibit the composer’s creativity or aesthetic choices.

The second section functions more like the development from a sonata than the contrasting central part of a ternary form. Here we chose specific materials and ideas from the opening to be explored further: the quasi-ostinato from bars 8-9 becomes a leading concept in the course of the development, while the use of a repeated chord progression (from bars 1-4) is also integrated freely in this segment.

It is important to note that dissonance, in the tonal sense, does not function in this style. In fact, certain intervals such as the major seventh and the tritone, which in the Common Practice needed some kind of resolution, here are primary characteristics of the vocabulary. Without a tonal hierarchy, pitches are defined in 12-tone composition only through their relationship to one another. As such, those with less compatible overtone series bring their contrasting profiles into greater relief and thus focus the sonority more acutely, whereas in Common Practice composition, pitches with more compatible overtone series reinforced the fundamental of a given tonal structure.

C. Rhythmic Dodecaphonic Piece

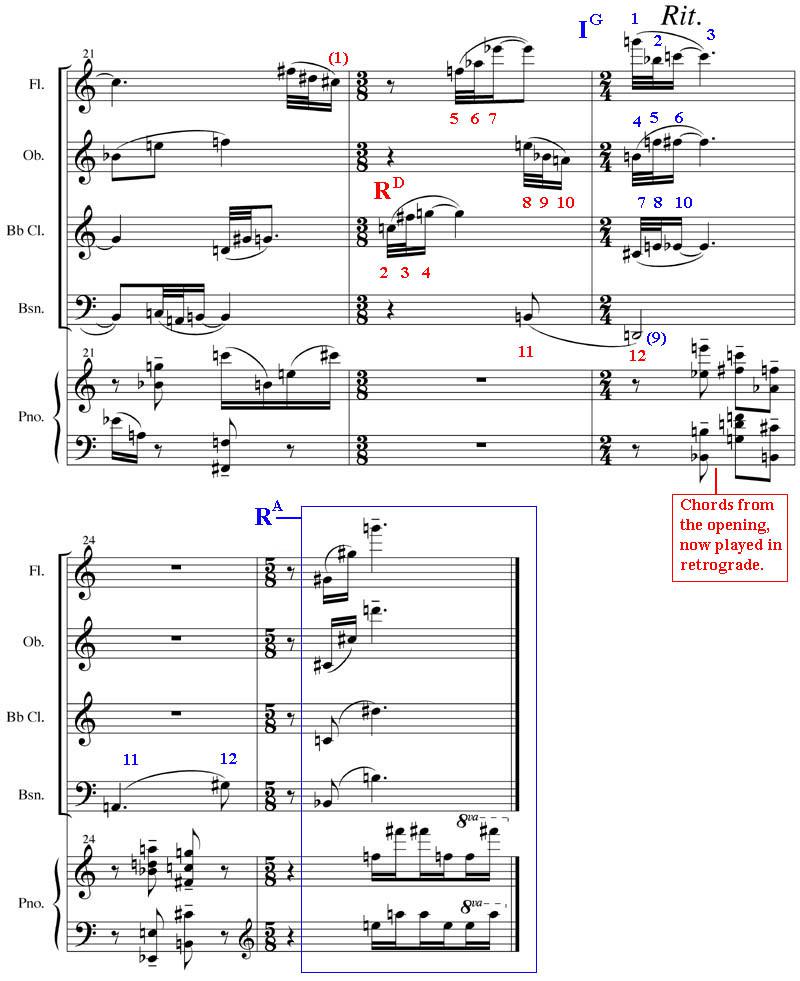
Rhythmic Composition. Here we will concentrate on exploring 12-tone composition utilizing primarily the polyphonic topography approach set in a bagatelle (a brief piece, usually of a capricious character). To elucidate the manner in which this method of implementing a dodecaphonic matrix can involve a multiplicity of row transformations simultaneously, we will write a chamber piece for winds and piano. In such a concise piece as this, the composition will concentrate on the interplay between just a handful of motifs and textural ideas.

Working with a series instead of a scale sometimes necessitates the composer concentrate on handling leaps rather than steps. As such, it is important to carefully gauge how to use large and dramatic leaps so that the ear of the listener does not tire. The same principles of how we hear a narrative in music apply as it does in traditional tonal music, despite the fact that the materials may be quite different. Composers of the Second Viennese School, including the aforementioned Arnold Schönberg and his pupil Anton Webern (1883-1945), initially borrowed forms from the Classical era for their nascent 12-tone ideas. This lent both composer and listener some familiar ground in which the new musical vocabulary could maturate.

As Webern’s particular style evolved, he often sought to apply symmetrical patterns to his musical ideas. This provides a key element to aid the listener in comprehension and also reflects the fundamental serial principle of retrogradable transformation. In a manner, Webern is telling us how to listen to this kind of music through a careful manipulation of the materials to incorporate basic 12-tone procedures into their inherent structures. We have endeavored to apply this concept, albeit sparingly, as in bars 5-7 (and again similarly in 19-21) wherein the piano articulates a pattern that is performed symmetrically.

A contrapuntal section based on interlacing imitative rhythms begins at bar 10 and concludes with a quasi-cadence at bar 14. The ensemble here contrasts the previous polyphonic web with a large ‘unison’ downward leap with all parts derived from one row.

Note that this distinct idea is used at the end of the piece with a final upward leap in all of the parts. These are the only instances of pure block topography in the piece.

Regarding how faithful we remain to the series precise, once again, we find occasions when there needs to be some degree of flexibility for our expressive requirements: in bar 4, the 9th note of the row that is being shared by the winds is skipped, while the final pitch in the piano is eliminated. The composition student must learn to always trust his/her musical instinct even if the system of choice prescribes something else.

Notes on Analysis:

The clarinet in Bb sounds as notated (for ease of reading).

Unlike the first piece, we have not analyzed every note but rather concentrated on illustrating significant aspects of the present work.