4.6 End-of-Chapter Exercises

Which of the following is not true about double-entry bookkeeping?

1. It originated in Italy.
2. Debits and credits must equal.
3. It is still used today.
4. An entry can have no more than one credit and one debit.

Which of the following entries could Yeats Company not make when they perform a service for a client?

1. Figure 4.20

   

2. Figure 4.21

   

3. Figure 4.22

   

4. Figure 4.23

   

Which of the following is a transaction for Tyler Corporation?

1. Tyler pays its employees $400 for work done.
2. Tyler considers renting office space that will cost $1,500 per month.
3. Tyler agrees to perform services for a client, which will cost $7,000.
4. Tyler places an order for supplies that will be delivered in two weeks. The supplies cost $200.

Elenor Company sells 400 units of inventory for $40 each. The inventory originally cost Elenor $26 each. What is Elenor’s gross profit on this transaction?

1. $16,000
2. $10,400
3. $ 5,600
4. $ 9,600

Which of the following increases with a debit?

1. Retained earnings
2. Sales revenue
3. Inventory
4. Note payable

In January, Rollins Company is paid $500 by a client for work that Rollins will not begin until February. Which of the following is the correct journal entry for Rollins to make when the $500 is received?

1. Figure 4.24

   

2. Figure 4.25

   

3. Figure 4.26

   

4. Figure 4.27

   

Record the following journal entries for Taylor Company for the month of March:

1. Borrowed $4,500 from Local Bank and Trust
2. Investors contributed $10,000 in cash for shares of stock
3. Bought inventory costing $2,000 on credit
4. Sold inventory that originally cost $400 for $600 on credit
5. Purchased a new piece of equipment for $500 cash
6. Collected $600 in cash from sale of inventory in (d) above
7. Paid for inventory purchased in (c) above
8. Paid $1,200 in cash for an insurance policy that covers the next year
9. Employees earned $3,000 during the month but have not yet been paid
10. Paid employees $2,900 for wages earned and recorded during February

For each of the following transactions, determine if Raymond Corporation has earned revenue during the month of May and, if so, how much it has earned.

1. Customers paid Raymond $1,500 for work Raymond will perform in June.
2. Customers purchased $6,000 of inventory for which they have not yet paid.
3. Raymond performed work for customers and was paid $3,400 in cash.
4. Customers paid Raymond $2,300 for inventory purchased in April.

Record the journal entries for number 2 above.

Determine the missing account balance in the following trial balance:

State which balance, debit, or credit is normally held by the following accounts:

1. Cash
2. Dividends
3. Notes payable
4. Unearned revenue
5. Cost of goods sold
6. Prepaid rent
7. Accounts receivable
8. Capital stock

Near the end of her freshman year at college, Heather Miller is faced with the decision of whether to get a summer job, go to summer school, or start a summer dress making business. Heather has had some experience designing and sewing and believes it might be the most lucrative of her summer alternatives. She starts “Sew Cool.”

During June, the first month of business, the following occur:

1. Heather deposits $1,000 of her own money into Sew Cool’s checking account.
2. Sew Cool purchases equipment for $1,000. The company signs a note payable for this purchase.
3. Sew Cool purchases $1,000 in sewing supplies and material in cash.
4. Sew Cool gives Heather’s parents a check for $80 for rent and utilities.
5. Heather sews and sells twenty dresses during the month. Each dress has a price of $60. Cash is received for twelve of the dresses, with customers owing for the remaining eight.
6. The dresses sold above cost $35 each to make.
7. Sew Cool purchases advertising for $50 cash.
8. Sew Cool pays Heather a cash dividend of $10 cash.

9. Sew Cool’s taxes, paid in cash, amount to $87.

   1. Prepare journal entries for the above transactions.
   2. Prepare T-accounts for each account used.
   3. Prepare a trial balance for June.

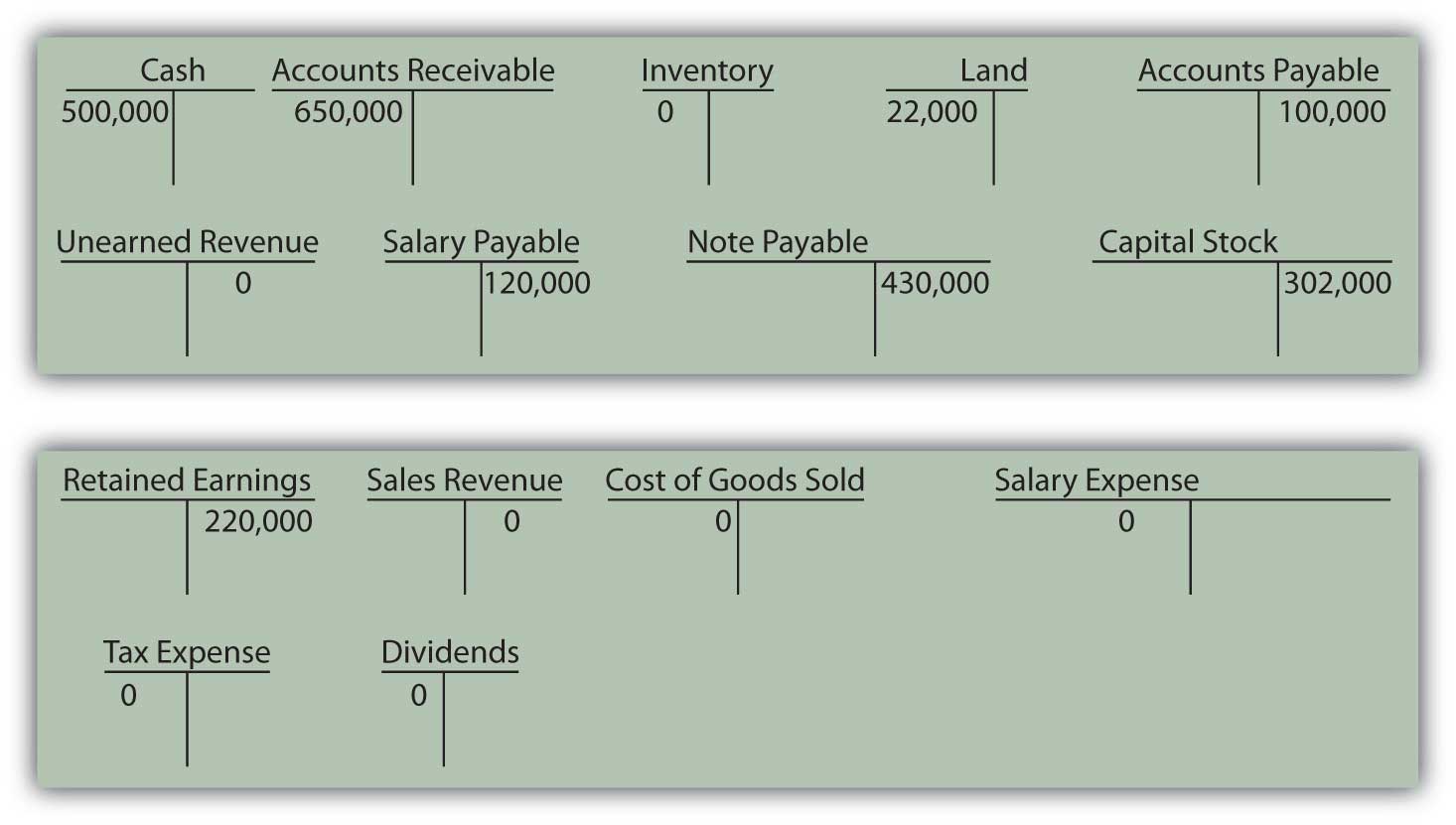
Bowling Corporation had the following transactions occur during February:

1. Bowling purchased $450,000 in inventory on credit.
2. Bowling received $13,000 in cash from customers for subscriptions that will not begin until the following month.
3. Bowling signed a note from Midwest Bank for $67,000.
4. Bowling sold all the inventory purchased in (a) above for $700,000 on account.
5. Bowling paid employees $120,000 for services performed during January.
6. Bowling purchased land for $56,000 in cash.
7. Bowling received $650,000 in cash from customers paying off January’s accounts receivable.
8. Bowling paid dividends to stockholders in the amount of $4,000.
9. Bowling owes its employees $123,000 for work performed during February but not yet paid.
10. Bowling paid $300,000 on its accounts payable.

11. Bowling paid taxes in cash of $45,000.

    Required:

    1. Prepare journal entries for the above transactions.

    2. Complete the T-accounts below. Numbers already under the accounts represent the prior balance in that account.

       Figure 4.29 Opening T-Account Balances

       

    3. Prepare a trial balance for February.

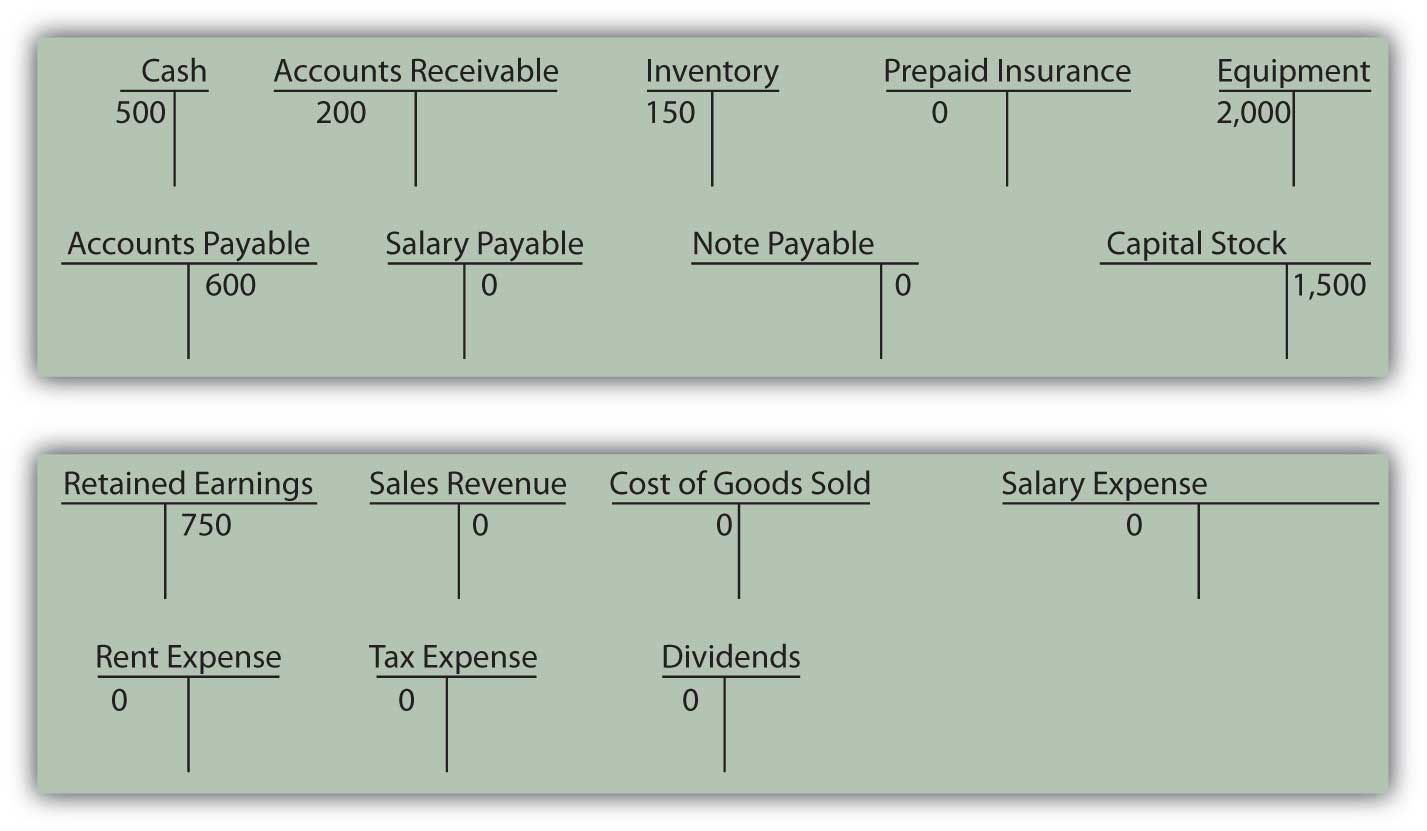
The following events occurred during the month of May for McLain Company.

1. McLain sells 240 units for $20 each. McLain collects cash for 200 of these units. The units cost McLain $8 each to purchase.
2. McLain purchases $1,800 worth of inventory on account.
3. McLain collects $500 in cash on its A/R.
4. McLain takes out a loan for $400.
5. McLain pays out $350 cash in dividends.
6. McLain receives a contribution of $600 from its owners.
7. McLain purchased a new piece of equipment. The new equipment cost $1,000 and was paid for in cash.
8. McLain pays $500 of its accounts payable.
9. McLain incurs $500 in salaries expense, but will not pay workers until next month.
10. McLain incurs $300 in rent expense and pays it in cash.
11. McLain prepays $200 in cash for insurance.
12. Taxes, paid in cash, are $110.

Required:

1. Prepare journal entries for the above transactions.

2. Complete the T-accounts below. Numbers already under the accounts represent the prior balance in that account.

   Figure 4.30 Opening T-Account Balances

   

3. Prepare a trial balance for May.