Chapter Sixteen: Explanatory Arguments

Sit down before fact as a little child, be prepared to give up every preconceived notion, follow humbly wherever and to whatever abysses nature leads or you shall learn nothing.

—T. H. Huxley, letter, September 23, 1860

Hypotheses and theories are not derived from observed facts, but invented in order to account for them.

—Carl Hempel, The Philosophy of Natural Science

Explanatory arguments are probably the most fundamental and frequently used of all arguments, both in science and in everyday life. Like their close cousins, inductive generalizations, explanatory arguments aim to expand our knowledge. But they differ from inductive generalizations in an important way. Both the premise and the conclusion of an inductive generalization are concerned with the same subject matter. Suppose, for example, that on a camping trip to the mountains you say to your friend, “This pot of water boiled quickly at this altitude; so all water boils quickly at this altitude.” The premise and conclusion are both about the boiling of water at this altitude. Explanatory arguments typically expand our knowledge by offering a different subject matter in the conclusion. Suppose your friend, having slept in the car during the trip and being unaware of the altitude, argues, “Hey, this water boiled quickly, so we must be well above sea level.” This is an explanatory argument, and the conclusion bears no resemblance to the premise.

Explanatory arguments require humble attention to the facts of our experience, as Huxley notes above. But, as Hempel suggests, that is not all they require—they require imagination. The arguer must have imagination to devise an explanation that is something more than a generalization of the experienced facts; and the evaluator must have imagination to think up viable alternative explanations for the sake of comparison.

As with the other argument forms introduced in this text, there are a variety of alternative terms for explanatory arguments, none of which seems to have taken the lead. The most common alternative is the term theoretical argument—in which, it is said, a theory is supported by appeal to facts. This terminology is acceptable but can be misleading, since many theories are quite factual and many facts are highly theoretical.^[1]

16.1 Correct Form for Explanatory Arguments

Explanations, to recall Chapter 2, are not necessarily arguments. Suppose on the camping trip your friend wonders why the water boiled so quickly, and you reply, “Because we are at a higher altitude.” This is not an argument. It is not offered as a reason to believe that the water boiled quickly. Why would you try to persuade your friend of something you have both just agreed is true? It is just an explanation, designed to make the unexpected experience easier to understand.

But when, having slept in the car, your friend says, “This water boiled quickly, so we must be well above sea level,” this is offered as a reason to believe that we are well above sea level. It is an argument. And it contains the two essential components of an explanatory argument. First, its conclusion—that we are above sea level—is an explanation. An explanation—also termed a theory or an explanatory hypothesis—is, for our purposes, loosely defined as a statement that enables us both to predict and to better understand the cause of that which it explains. Second, its explicit premise—this water boiled quickly—is the observable outcome of the explanation. The observable outcome—also termed the data, the prediction, or the facts—follows from the explanation and can in a certain way, at a certain time, and under certain conditions, be seen, heard, smelled, tasted, or touched.

The correct form for an explanatory argument, assuming that P is the explanation and Q is the observable outcome, is this:

The first premise, often implicit, states that the explanation enables you to predict the observable outcome—that it really is an outcome. The second premise states that the observable outcome is known to have happened—that it has been observed. The argument concludes with the assertion of the explanation. The mountain argument can be clarified roughly as follows:

For a more substantial example, let’s look at a famous explanatory argument from science.^[2] In 1687, Isaac Newton published his monumental Principia. It included an account of the physical laws that govern the interactions of the planets, stars, and other heavenly bodies. The physics of Descartes still dominated science, and it would be several decades before Newton’s views completely won out. In 1695, Edmund Halley began to ponder whether Newton’s account of celestial mechanics was correct and, in particular, whether it applied to the motion of comets. To simplify, Halley wondered about the following statement:

Newton’s account of celestial mechanics is correct and, in particular, applies to the motion of comets.

So far as anyone at the end of the 17th century had been able to tell, the motion of comets was utterly irregular. But if Halley was right about Newton’s views, there would be detectable regularities—certain comets would be found to follow fixed elliptical orbits around the sun.

Halley was especially interested in a comet he had observed in 1682. After much research, he found that comets with similar orbits had also been observed in 1530 and in 1606. Applying Newton’s laws to these data, he boldly made the following prediction:

A comet with an orbit similar to the 1530 and 1606 comets will appear in December 1758.

It was a remarkably precise prediction—preposterous, really, given the rarity of comets, unless one made the assumption of Newton’s celestial mechanics. As the decades passed it was not forgotten, and the comet appeared on Christmas Day, 1758. Some historians mark this as the day of the final triumph of the Newtonian over the Cartesian theoretical tradition.

The sentence Newton’s account of celestial mechanics is correct . . . serves here as an explanation of the otherwise unpredictable appearance of the comet on Christmas Day of 1758. The sentence A comet with an orbit similar to the 1530 and 1606 comets will appear in December 1758 is the observable outcome, that which the explanation enables us to predict and to better understand. The comet argument can be clarified as follows:

16.1.1 The Fallacy of Affirming the Consequent

The correct form for an explanatory argument should look familiar—it is also the form of the fallacy of affirming the consequent, introduced in Chapter 11. Does this mean that explanatory arguments are always fallacious? No. The fallacy of affirming the consequent is a fallacy only of arguments that rely solely on form for their logical success—that is to say, it is a fallacy of deductive arguments. But explanatory arguments are inductive arguments. They must satisfy the correct form condition, but, like every other inductive argument, they would be logical failures were that their only success; they must also satisfy the total evidence condition. This condition is the logical requirement on any inductive argument that its conclusion fit appropriately with the total available evidence.

In practice, it is usually easy to tell the difference between an explanatory argument and a deductive argument. Is the if-clause intended to provide a better causal understanding of the then-clause? Is the if-clause offered as superior to alternative explanations of the then-clause? Then it is an explanatory argument. On the other hand, does the arguer seem to expect the form alone to provide the logical support for the conclusion? Then it is a deductive argument and commits the fallacy of affirming the consequent.

Suppose I say to you, “If he is from Chicago, then he is from Illinois—and he is indeed from Illinois, so he must be from Chicago.” You can’t be absolutely sure without some wider context, but it normally wouldn’t make sense for me to explain someone’s residency in Illinois by pointing to his residence in Chicago. If I were trying to give you a better causal understanding of it, you would probably expect me to tell you something about the chain of events—the family history or career decisions—that led him to Illinois. So an argument of this sort is probably just a logical mistake, not an explanatory argument.

It can also be helpful to know that when explanatory arguments occur in ordinary language, the if–then premise is more often than not implicit (which tends not to be the case with the fallacy of affirming the consequent). And, though you may not find the if–then premise, there are two things you can always expect to find if the argument is explanatory: reference to the explanation, often with a discussion of why it is better than alternative explanations; and reference to the observable outcome, often with a discussion of how unlikely that outcome would otherwise
have been.

That a deductive failure and an inductive success can share the same form reminds us of an important lesson: deductive arguments rely only on the correct form condition, while inductive arguments also have recourse to the total evidence condition. A form that cannot pull any of the load in a deductive argument may nevertheless pull a share of the load in an inductive one.

16.1.2 The Variety of Explanatory Arguments

Explanatory arguments come in several varieties. Two ways of distinguishing them—according to chronology and to generality—can be especially helpful.

The first point of distinction is chronological. In many cases, an explanation is formulated before the observable outcome has been observed. Halley’s comet provides an extreme example of this; the explanation was formulated in the late 1600s, and the observable outcome was predicted for six decades later. Often, however, the chronological order is reversed; the observable outcome is observed, then the explanation fashioned in response to it. If you find a dead body, for example, with assorted fingerprints on the candlestick, you are beginning with the observable outcome; only later does the detective invent the explanation that the butler did it. Here is an example from Arthur Conan Doyle’s A Study in Scarlet; Dr. Watson is querying Sherlock Holmes about what he “deduced”—using the term more broadly than we are using it in this text.

“How in the world did you deduce that?” I asked. “Deduce what?” said he, petulantly. “Why, that he was a retired sergeant of Marines.” “. . . Even across the street I could see a great blue anchor tattooed on the back of the fellow’s hand. That smacked of the sea. He had a military carriage, however, and regulation side-whiskers. There we have the marine. He was a man with some amount of self-importance and a certain air of command. You must have observed the way in which he held his head and swung his cane. A steady, respectable, middle-aged man, too, on the face of him—all facts which led me to believe that he had been a sergeant.” “Wonderful!” I ejaculated.

Unlike the case of Halley’s comet, the observable outcomes—a blue anchor on his hand, a military carriage, regulation side-whiskers, an air of command—are where the reasoning begins. The explanation—that he was a Marine sergeant—comes next. Nevertheless, we clarify and evaluate the argument just like the comet argument. Here is one good way of clarifying it:

From a logical point of view, the chronological relationship between the two does not matter. We make our observations when we can and we fashion our explanations when they occur to us, and the same principles of evaluation apply regardless of which comes first. Practically speaking, however, explanations that do precede their observable outcomes are often logically stronger. It is easy to invent a convenient explanation for data you already have, but then to disregard failure to fully satisfy the total evidence condition. It is much harder to invent an explanation that successfully predicts future observations. You should be a bit more suspicious of explanatory arguments in which the observable outcome preceded the explanation—but for psychological, not logical, reasons.

A second way of distinguishing among explanatory arguments is in their level of generality. General explanations—Newtonian celestial mechanics, for example—are intended to apply broadly; Newton’s theories explain the motion of all heavenly bodies at all times. Such arguments are typical of science, though are not restricted to it. Singular explanations—that the butler did it, or that the man was a Marine sergeant—are designed to apply to a very specific thing or event—to this particular murder or to that particular man’s physical characteristics. Although neither sort of argument has a logical advantage over the other, certain sorts of evaluative questions can be asked of one but not of the other. For example, we can ask about the frequency of singular explanations—how frequently butlers leave their fingerprints on candlesticks or how frequently marines have tattoos—but it isn’t helpful, probably not even meaningful, to ask about the frequency with which Newtonian mechanics is true.

16.2 The Total Evidence Condition (1): The improbability of the Outcome

As we have seen in the preceding chapters, the conclusion of a strong induction must fit both the premises and the available background evidence. For explanatory arguments there are two main parts to the total evidence condition: the outcome must be sufficiently improbable and the explanation must be sufficiently probable. In this section we will look at the improbability of the outcome.

16.2.1 The Outcome Must Be Sufficiently Improbable

No one would have expected a comet in December 1758 unless they were assuming the Newtonian explanation; such an event would have been extremely improbable. This is an important source of the comet argument’s logical strength. If comets were common in December, then the premises of the argument would have still been true, but they would have given us no good reason to believe the conclusion. If the comet had been expected anyway, why should its appearance point toward Newtonian mechanics as opposed to whatever was the already accepted explanation? Similarly with our other cases. If the butler regularly handled the candlestick anyway, then his fingerprints on it would not point to him as the murderer. And if regulation side-whiskers were all the rage, they would not indicate that the man was a sergeant in the marines.

The first part of the total evidence condition is that the observable outcome must have a low prior epistemic probability. Epistemic probability, as explained in Chapter 9, refers to the probability of the statement’s truth given all relevant available evidence. The term prior, in this case, means that the probability calculation must be done prior to your making any judgment about the explanation itself and prior to your making any observations pertinent to the observable outcome. In other words, it means that you cannot use all of the relevant available evidence in making this particular judgment—you must exclude the assumption that the explanation is true, and you must exclude observations that might have already been made in the attempt to verify premise 2.

This makes good sense. If you evaluate the probability of the appearance of the comet but include in your background evidence the assumption that Newton is correct, then (setting aside the problem this would probably be the fallacy of begging the question) the probability of the 1758 comet would be very high—it is, after all, derived from the Newtonian explanation as its outcome! Again, if you include the observations actually made in December of 1758, the probability would be very high—they saw it!

Why is this criterion important? If the prior probability of the outcome is high, then we expect the outcome to happen anyway—even if the hypothesis is false. Suppose Halley had decided to look for confirmation of Newton’s celestial mechanics by studying the sun rather than comets and, based on Newton, had confidently predicted that the sun would rise the next day. It is not likely that we would now call it Halley’s sun. When the outcome already has a high prior probability, the hypothesis does no work. The work is being done by whatever independent reason we already have for expecting the outcome to occur.

Some writers refer to this as the surprise criterion; it tests to see if you would be surprised by the outcome were you not to assume the explanation. The more surprising the outcome would be, the lower the prior probability and the stronger the logic of the argument. This can be a useful standard, but remember that surprise is a psychological condition—thus, strictly speaking, it is an indicator of low subjective, rather than epistemic, probability. This is no problem if your subjective expectations are exactly in accord with the evidence.

Unfortunately, there is no formula for calculating the prior probability of the observable outcome. There are, however, several helpful strategies that you can follow in making your judgment.

16.2.2 Reject Unfalsifiable Explanations

It isn’t possible to say with precision how improbable the outcome must be to count as sufficiently improbable. But it is possible to specify the lowest hurdle that must be cleared. The explanation must, at a minimum, be falsifiable. Falsifiability applies when there is some possible observable outcome of the theory that could prove the explanation to be false. Suppose I am encouraging you in your fledgling acting career and argue, “You are so talented that all the critics who don’t praise you are just jealous. I know that all the critics panned your opening performance last night. But that proves my point.” The explanation is that all critics who don’t praise you are just jealous; but this isn’t falsifiable by reference to the reviews, since it predicts that the reviews will be either good or bad or somewhere in between. But it is highly probable, whether my theory is true or false, that the reviews will be good or bad or somewhere in between. So my jealousy explanation flunks the test for low prior probability.

Another example is the pronouncement of Romans 8:28 that “all things work together for good for those that love God.” Some Christians will take any outcome at all to be, in some sense or other, good and thus to be evidence for the truth of this saying. When desperately needed money arrives mysteriously in the mail, that is support for Romans 8:28. When your entire family is wiped out in a car crash, that is support for Romans 8:28 too—after all, they are in heaven and you are going to have your character strengthened, so it is good. This interpretation of the saying is unfalsifiable and can receive no logical support from the nature of one’s experience.

To put it more generally, to say that an explanation or an outcome is unfalsifiable is to say that any observation at all is consistent with the explanation. And it is highly probable that we will have “any observation at all.” Any unfalsifiable explanation is in principle unable to satisfy the improbable-outcome criterion and can never be the conclusion of a sound explanatory argument. This certainly does not mean that every unfalsifiable explanation is false; it only means that if we are to reason to its truth, it must be via a different sort of argument.

16.2.3 Favor Precise Outcomes

Although there is no formula for deciding on the improbability of the outcome, there are some helpful strategies that you can follow in making your decision.

One good way to check for an improbable outcome is to ask this: Is this outcome so vague that it might well be true anyway? Recall, from Chapter 13, that larger margins of error make it much more probable that the conclusion of an inductive generalization is true; there is a much greater chance that between 50 percent and 60 percent of the voters favor Jones than there is that exactly 55 percent of them do. This point can be broadened: vague statements, in general, are more likely to be true than precise ones. Halley’s job would have been much easier if, instead of predicting a comet precisely in December 1758, he had made the following vague prediction:

At least one comet will appear somewhere in the sky at some time in the future.

This observable outcome easily follows from the Newtonian explanation—thus, it would provide us with an argument with true premises. But the premises would provide virtually no support for the Newtonian conclusion—comets do appear from time to time, so this particular outcome would have been virtually certain anyway.

In ancient Greece, when there was a difficult decision to be made, the wealthy Greeks would sometimes travel to Delphi and consult the oracle there—an oracle who, it was believed, had special powers to foresee the future. The oracle tended to utter solemn pronouncements of a very unspecific sort—for example, “I see grave misfortune in your future.” It was almost inevitable that such a vague prediction would come true. For the Greek might count anything as grave misfortune, from a financial reversal to the death of an aged parent. When it did come true, it was often counted as reason to believe that the oracle had special powers. But the extremely high prior probability of the outcome renders the argument logically useless. For exactly the same reason, we can hardly consider astrology to be supported when someone finds that the day’s horoscope has some truth in it; horoscopes are worded so vaguely that there are almost always events that can be interpreted as making them true.

The problem in all of these cases is that the explanation does no work. It is freeloading; so it deserves no credit when the outcome comes true.

16.2.4 Favor Outcomes for Which No Explanation Already Exists

Another good way to check for an improbable outcome is to ask this: Does another explanation for this outcome already exist? Included among your background evidence may be a belief that already serves as a perfectly good explanation for the outcome—in which case, you would expect the outcome anyway. This is why, for example, we are amused but not persuaded by the rooster who thinks that the sun is raised each morning by his mighty crowing. Another explanation for the sunrise already exists in our own background evidence—that the earth is rotating on its axis.

More subtle examples are easy to find. Wilson Bryan Key, whose most famous book was titled Subliminal Seduction, has argued that Madison Avenue strategically permeates its advertisements with camouflaged sexual images that are invisible unless you look very hard for them. For example, an unnoticed erotic image on a Ritz cracker, Key says, “makes the Ritz cracker taste even better, because all of the senses are interconnected in the brain.” The problem with his argument is that another explanation for these “unnoticed images” already exists; we all know that we’re capable of finding images if we look really hard for them, simply as the products of our imagination. His argument would gain some logical strength if, when we looked for them, we could find sexual images in advertisements more often than we find them in the clouds. Until then, the argument is no better than a product of Key’s own imagination.

An even subtler example can be found in academic discussions of the theory that punishment motivates learning better than does reward. The experience of flight instructors was at one time taken to be good evidence for the theory. Instructors found that when a student pilot was scolded for a poor landing, the student usually did better the next time. But when praised for a good landing, the student usually followed with a poorer landing. The argument might be clarified as follows:

Then someone realized that this sort of evidence provided no logical support for the conclusion. For the observable outcome of premise 2 is something that we would fully expect, even if the explanation were false. Why? At any given time, each pilot has achieved a certain level of competence—call it the pilot’s current mean level of competence. Any performance significantly better or worse than the student’s current mean level of competence would be largely a matter of chance. After significantly departing from the mean level of competence, we would expect that the next attempt would be closer to the current mean. This means that an unusually good performance would typically be followed by a poorer one—returning downward to the mean—and that an unusually bad performance would typically be followed by a better one—again returning to the mean, but this time upward. The scolding and praise are no better than a fifth wheel in the argument, since the outcome is highly probable anyway. Because the explanation does no work in making the outcome probable, it should get none of the credit when the outcome is observed.

16.2.5 Favor Outcomes that Would Falsify Alternative Explanations

Another good way to check for an improbable outcome is to ask this: Does this outcome rule out the leading alternative explanations? The philosopher Francis Bacon wrote four centuries ago of this experience:

When they showed him hanging in a temple a picture of those who had paid their vows as having escaped shipwreck, and would have him say whether he did not now acknowledge the power of the gods, —“Aye,” asked he again, “but where are they painted that were drowned after their vows?”

The explanation here is The gods are powerful and the observable outcome is Many who worship the gods have escaped from shipwrecks. But there is a viable alternative explanation for this outcome—namely, Escaping from a shipwreck is largely a matter of luck, shipwrecks having little regard for passengers’ religious beliefs. The logic of the gods argument would benefit if its observable outcome ruled out the luck alternative—if, for example, the outcome were revised, as Bacon hints, to this: Nobody who worships the gods has drowned in a shipwreck. Partly because this revised outcome would be false, it has not been offered; so the argument is handicapped by an outcome that leaves the luck alternative still standing. So the outcome probably would be true even if the gods explanation were false, and the argument is logically extremely weak.

Favoring outcomes that rule out alternative explanations is an especially powerful strategy. For, as researchers have shown, we have a natural tendency—termed a confirmation bias—to look for outcomes that support our preferred explanation rather than those that might falsify the alternatives—to look, for example, for worshippers who escaped rather than thinking also about those who drowned.

To illustrate this bias, suppose I tell you that I have in mind a set of numbers that includes the numbers 2, 4, and 6, and I then ask you to guess what set of numbers I am thinking of. You probably already suspect that it’s the set of all even numbers; but before I make you commit to that answer, I offer you the opportunity to test your answer by suggesting one more number that is either in or out of the set. If you are like most people you suggest, “Eight is in the set.” And my reply is that yes, 8 is included, because I am thinking of the set of all whole numbers. You can now see that you squandered your one opportunity. Influenced by the confirmation bias, you proposed a number that would confirm your preferred answer. But you would have done far better to propose, “Seven is not in the set.” If you had been right, you not only would have confirmed your preferred even-numbers answer, but also you would have ruled out the whole-numbers alternative—thereby improving the logical support for your answer. And if you had been wrong—and you would have been wrong—you would have had the chance to correct the error of your ways.

To illustrate how this strategy is related to the prior epistemic probability of the outcome, suppose I propose the following fanciful explanation:

I am bewitched, so that gravity has no affect on me whatsoever; the only reason I am able to walk around on the ground is because of magical shoes that counteract the bewitchment when I wear them.

My evidence? I offer the observable outcome that I walk around on the ground while I wear the shoes. And so I do. But this outcome provides no support for the explanation. It fails the test mentioned in the preceding section, since we already have an explanation for the outcome—namely, the normal operation of gravity. The argument would be greatly improved if the outcome included an attempt to rule out this alternative explanation, namely, I walk around on the ground while I wear the shoes, and I float in the air when I take them off. If this turns out to be true, it provides much better support for the explanation since it rules out the gravity alternative. An observable outcome for which there are fewer possible explanations is that much more improbable—and, thus, is that much logically stronger.

This helps to explain why so-called anecdotal evidence can be problematic. Suppose I have heard that vitamin C prevents colds; I don’t know whether to believe it but decide it’s worth looking into. I presume:

1. If vitamin C helps prevent colds, then when I take a lot of vitamin C I get fewer colds than normal.

I do take a lot of vitamin C over the winter and get only one or two colds, though I usually get three or four. So I add the premise,

2. When I take a lot of vitamin C I do get fewer colds than normal.

I then conclude,

My argument may provide a small measure of logical support for its conclusion, but what it does not do is rule out the following alternative explanations:

• The reduction in my colds was simply a coincidence.
• I was being more careful about my health because I was engaged in the experiment.
• I subconsciously wanted the test to succeed, so I tended not to count less severe colds that I otherwise would have counted.

A more careful test of the same theory would rule out these alternatives by using two large groups—one group that receives Vitamin C and a control group that receives a placebo—in a double blind test. (It is called double blind because neither those receiving the pills nor those administering the study knows which group is getting the real Vitamin C and which is getting the bogus Vitamin C.) By using large groups, the coincidence alternative is ruled out. By using the control group, the alternative is ruled out that the effect is somehow induced by the test itself. And by using a double blind test, the alternative is ruled out that the data were being interpreted differently for each group.

This argument would have the same form as the first one, differing only in the nature of the observable outcome.

Because the observable outcome rules out the leading alternative explanations, its prior probability is far lower than the anecdotal argument—and thus the argument is logically much stronger.

16.3 The Total Evidence Condition (2): The Probability of the Explanation

16.3.1 The Explanation Must Be Sufficiently Probable

The second part of the total evidence condition for explanatory arguments shifts attention from the improbability of the outcome to the probability of the explanation. As with the outcome, the concern here is also with prior epistemic probability—in this case, the probability that you would assess to the explanation prior to your making any judgment about the observable outcome. This makes good sense, because the probability of the explanation after you make a judgment about the observable outcome would roughly be your assessment of the soundness of the argument and it is too soon to make that judgment. Further, it is not necessary for the prior probability of the explanation to be high; if the explanation were already highly probable, there would be no need for the argument! Rather, it is simply necessary that it not be implausibly low and that it be higher than that of the leading alternative explanations.

The second part of the total evidence condition requires that you exercise the same imaginative powers as the arguer; for you must imagine which explanations would be the most credible alternatives to the one argued for. We typically favor the explanations with the highest prior probability. A house fire victim, for example, is quoted in the newspaper as explaining, “I kept smelling something, and then I saw the smoke. I thought somebody must be barbecuing. I couldn’t believe it was a fire. After a few seconds, I knew it was.” Barbecues occur far more frequently than house fires, so they have a much higher prior probability; but when the observable outcome—way too much smoke—does not follow from the barbecue explanation, we are logically forced to the less probable explanation that it is a house fire.

But sometimes the more probable explanation does not occur to us—we need more imagination or, perhaps, a better education. When he was a young lawyer, Abe Lincoln had to defend a client against a case that seemed to be strongly supported by a list of undisputed facts. In summing up his defense before the jury, he said, “My esteemed opponent’s statements remind me of the little boy who ran to his father. The lad said that Suzy and the hired man were up in the hayloft—that Suzy had her dress up and the hired man had lowered his trousers. ‘Pa!’ exclaimed the youngster, ‘they are getting ready to pee on the hay!’ ‘Well, son,’ replied the father, ‘you’ve got the facts all right, but have reached the wrong conclusion.’” Lincoln’s client, we are told, was acquitted. Part of the reason, presumably, was because the jury saw that if they carefully thought about alternative explanations, they might find one with a higher prior probability than the one Lincoln’s opponent was arguing for.

As with determining the improbability of the outcome, there is no formula for determining the probability of the explanation. There are, however, several useful strategies that we will discuss next.

16.3.2 Favor Frequency

For singular explanations—such as The butler did it or This man was a Marine sergeant—the best question to ask is this: Is this sort of thing known to occur, and does it occur more frequently than do the leading alternatives? Suppose the phone rings and you pick it up, only to hear the “click” of someone’s hanging up on the other end. “Aha!” you say, “Someone is casing the joint and now knows not to burglarize us, since someone answered the phone!” This explanation is the sort of thing that is known to happen—burglars do sometimes call ahead to see if anyone is home—so it is not implausibly low. But the problem is that there is at least one alternative explanation that occurs much more frequently. Consider the alternative that someone has accidentally dialed a wrong number, only to hang up when hearing an unfamiliar voice on the other end. Which occurs more frequently—burglars or butterfingers? Butterfingers, of course. So the logic of the burglar argument is shown to be weak.^[3]

This can be a powerful evaluative tool. Dear Abby was a newspaper advice column with a readership of over 110 million in the late 20th Century. Here is one of the classic exchanges:^[4]

Dear Abby: I’m a traveling man who’s on the road five days a week. I have a pretty young wife (my second) whom I’ve always trusted until last Friday night when I came home, put on my bathrobe and found a well-used pipe in the pocket! I don’t smoke a pipe. Never have. And my wife has never smoked anything. She claims she has never seen that pipe before and doesn’t know how it got there. OK, so she’s not admitting to anything, but the next day when I went to get the pipe, it wasn’t where I had put it! It just plain disappeared. I searched the apartment, but it was nowhere to be found. My wife claims she doesn’t know what happened to it. We are the only two people in this apartment. From what I’ve told you, what conclusions would you draw? No names, please. My wife calls me—Papa Bear

Dear Papa Bear: It’s just a wild guess, but I think somebody’s been sleeping in your bed. Pity, the evidence went up in smoke.

About a month later this letter appeared—really:

Dear Abby: The letter from the traveling man who spends five days a week on the road interested me. He said he came home to discover a well-used pipe in the pocket of his bathrobe. . . . Well, Abby, this should clear up the mystery of MY missing pipe. Being a plumber, I was summoned to the home of an attractive woman to repair a faulty shower nozzle that was spraying water all over her bathroom. While waiting for my clothes to dry, I slipped into a robe hanging on a hook in the bathroom, and I must have thoughtlessly put my pipe into the pocket. After searching for it high and low later, I suddenly remembered. When I went back to that house, the door was open and I could hear a loud argument coming from another room, so I sneaked in and quietly retrieved my pipe. I hope this explains it for all hands. Pete McG. P.S. Could you find out for me which five days that man is on the road?

Dear Pete: Sorry, no help from this corner for a plumber who can’t keep track of his pipes.

Abby’s explanation is that the wife is having an affair; the observable outcome is that the pipe unexpectedly appears and then mysteriously disappears. But the second letter, using the same observable outcome, offers an alternative explanation—namely, that a plumber visited, left the pipe, then surreptitiously retrieved it.

How does Abby’s conclusion fare in the face of this alternative explanation? Not too badly, if we compare the frequencies of each. The plumber explanation is burdened with improbabilities:

• How often do people call an expensive plumber over a faulty shower nozzle when it could be easily unscrewed and replaced with a $5 part?
• How often do people leave water spraying everywhere rather than simply turning it off?
• How often do plumbers leave water spraying everywhere rather than turning it off—if not at the faucet, then at the main?
• How often do plumbers waste time by doing things such as drying their clothes when they can make more money by going on to another job?
• How many plumbers smoke pipes?
• The husband said he put the pipe somewhere, and the plumber had no way of knowing where; how often is someone going to be able to sneak in and find something like that without being caught?
• The plumber says he went to a house, while the man says he lives in an apartment; how often does someone make that sort of mistake?
• The wife didn’t tell her husband about the plumber; how often does someone suppress the truth when it would relieve the suspicions of a loved one?
• The plumber could’ve called the man or sent a note (enclosed, perhaps, with his bill) to straighten things out, but wrote Dear Abby where there was a good chance it wouldn’t be published or the man wouldn’t read it; how often does a well-intentioned person take such an ineffective action to right a wrong?

The answer in each case is very infrequently. When we compare frequencies we see that the prior probability of each portion of the plumber explanation is quite low; and the conjunction of all portions (recall Chapter 10—this requires that the probabilities of all the parts be multiplied) is far, far lower. Clearly, the plumber explanation has a much lower prior probability than does the affair explanation. Abby’s argument remains moderately strong.

16.3.3 Favor Explanations that Make Sense

General explanations—such as Newtonian mechanics applies to the motion of celestial bodies or Vitamin C helps prevent colds—do not lend themselves to the question about comparative frequencies because they are general. But you can still ask whether such explanations make sense, and whether they make more sense than the alternative explanations. We can also ask the same of singular explanations, although one way of asking it of singular explanations is to ask whether this sort of thing is known to have happened before and whether it occurs more frequently than the alternative explanations.

Another way to put this is to ask whether there is a satisfactory conceptual framework for the general explanation—and whether it is more satisfactory than the alternatives. Would it require the world to function in mysterious ways or in ways that differ dramatically from the ways that are well established by science? If so, it is probably better to judge the logic of the argument as, at best, undecidable and, at worst, extremely weak. It must be emphatically added that the world is in many ways mysterious, and that science can be mistaken, and often is. But explanatory arguments that rely heavily on mystery or that depend on the overthrow of science cannot be considered successful until they do the hard work of filling in the blanks. If there are too many blanks, then the explanation’s prior probability is too low for the argument to be logically strong.

Examples of this abound, even in some of the most widely accepted explanatory theories. Many smart people refused at first to wholeheartedly endorse Newtonian mechanics because it lacked a satisfactory conceptual framework in one important respect. It assigned a central role to gravity, which is, in effect, action at a distance; but it did not offer any account of how gravitational forces can act across space without any intervening physical bodies. Due to this defect, it took an especially rich array of observable outcomes and an especially compelling theoretical simplicity for it to gain rational acceptance. In another example, continental drift initially was reasonably rejected as the explanation for the striking biological and geological similarities between continents that are widely separated by oceans because there was no known mechanism for the drift. But the theory of plate tectonics eventually provided a conceptual framework for continental drift, and the explanation no longer has an unacceptably low prior probability. Meteorites provide yet another example. Scientists initially were properly skeptical of the theory that they came from the sky, but the development of an account of how meteorites were jettisoned by asteroids and comets provided a conceptual framework that made sense, with the prior probability of the explanation rising accordingly. (The Vitamin C example is similar; one reason that researchers have not worked harder at collecting evidence for the theory is because it is unclear how it would work. Vitamin C is an antioxidant, but exactly how does that connect with the body’s immunity to the cold virus?)

When established scientists reject offbeat theories, defenders of such views love to cite these cases. Scientists rejected Newton, they rejected continental drift, they rejected meteorites, and they were wrong! So the scientists are wrong when they reject the paranormal, ancient astronauts, and homeopathic medicine! Scientists were right to reject these formerly offbeat views until they could make good sense of them, and they will be right to reject the paranormal, ancient astronauts, and homeopathic medicine until they can also make good sense of them. Some explanations will eventually measure up to the standards of good reasoning; that is no reason to eliminate the standards.

16.3.4 Favor Simplicity

Simplicity can be a significant contributor to the probability of an explanation. The point is not that the world is necessarily simple, any more than the world is necessarily filled only with frequently occurring or nonmysterious things. The point is that, other things being equal, simple explanations, like frequently occurring and nonmysterious explanations, have a higher prior probability. An explanation is in this way like a machine. Some machines require a large number of moving parts to work properly. But the more moving parts a machine has, the more likely it is that it will break down—so a well-designed machine includes no more parts than absolutely required.

This applies to both singular and general explanations. One good way to check for simplicity—a way typically more useful with singular than with general explanations—is to ask whether the explanation offers only as many explanatory entities as needed. When faced with the dead body and the candlestick bearing the butler’s fingerprints, even if there were no evidence pointing toward the chambermaid, an alternative explanation might have been this:

The butler and the chambermaid committed the murder together, but only the chambermaid was wearing gloves.

The observable outcome follows from this explanation just as well as it does from the explanation that it was merely the butler who did it, but the simpler butler explanation has a higher prior probability. Why? Suppose the prior probability that the butler did it was .10, likewise for the chambermaid. Then, recalling our discussion of evaluating the truth of both–and sentences in Chapter 10, the prior probability that it was both of them can be roughly understood as .10 times .10, or .01. Add a moving part to the machine, and the probability that every part will work drops dramatically.

This interlocks with the test, under the preceding improbable-outcome criterion, of asking whether an explanation for the outcome already exists. When an explanation already exists, the arguer is free to respond in, for example, the case of the student pilots’ performance, “OK, but this outcome is explained both by the efficacy of punishment and by the normal return to the current mean after an aberrant performance.” But now it violates the second part of the total evidence condition as well!

For general explanations, a good way to check for simplicity is to ask whether the explanation predicts the smoothest possible curve.In the 17th century, the Italian mathematician Torricelli hypothesized that the Earth was surrounded by a sea of air, which decreased in pressure uniformly as the altitude increased. Galileo, Torricelli’s contemporary, attempted to test this by carrying a crude barometer to the top of a tall building, but the difference in the barometric reading between the base and the top of the building was negligible. Another contemporary of his, French mathematician and philosopher Blaise Pascal, suspected that Torricelli was right but that a greater altitude was required to prove it. Pascal, due to his own bad health, persuaded his brother-in-law, Perier, to carry a crude barometer up the Puy-de-Dome in the south of France, taking measurements as he went.

Perier stopped and measured the barometer from time to time as he scaled the mountain, with results that were widely taken as impressive proof of Torricelli’s hypothesis. The reading in Paris, at sea level, was 30 inches; at the base of the Puy-de-Dome, at 1,300 feet, it was about 28.7 inches; and at the mountain’s peak, at 4,800 feet, it was about 25.2 inches. For the sake of illustration, I will slightly idealize the intermediate readings: say, it was 28.2 inches at 1,800 feet, then one inch lower at each of the next thousand-foot intervals.^[5] A graph of these results, representing our evidence in this case, looks like this.

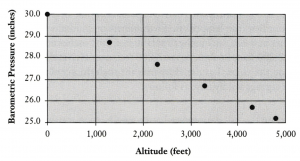
The argument might now be clarified as follows:

Given that the explanation calls for a uniform decrease in air pressure, it would then predict that if samples were taken at all other altitudes on the Puy-de-Dome, they would be plotted on the graph along a line described by the smoothest curve that can be drawn through the points already there, as follows.

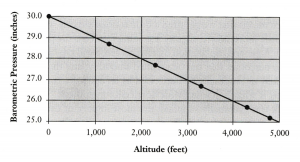
But suppose I offer the alternative explanation that air pressure is highly irregular but that it so happens that barometric pressure nevertheless would be 30 inches at 0 feet, 28.7 inches at 1,300 feet, 28.2 inches at 1,800 feet, 27.2 inches at 2,800 feet, 26.2 inches at 3,800 feet, and 25.2 inches at 4,800 feet. The line on the chart, I argue, does pass through the six plotted points but otherwise zigzags wildly, say, as follows.

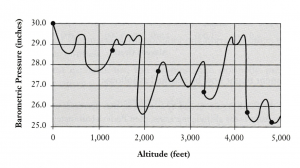
Both explanations do an equally good job of entailing Perier’s results as their observable outcome. But the first one, Torricelli’s, has a higher prior probability because it is simpler, due to its prediction of a smoother curve.

The simplicity test, as explained here, is related to the makes-sense test. As we have seen, explanations that make good sense are those for which we have an adequate conceptual framework—for which we have a reasonably good account of the causal mechanisms involved. Further, we suppose that causal mechanisms operate uniformly in the world—that under similar circumstances they operate similarly, and that slight dissimilarities in circumstances tend to produce slight dissimilarities in the way they operate. Slightly less oxygen means that we get tired a little sooner; slightly worn brakes stop the car a little more slowly; slightly less sunlight means the plant grows a little shorter. A general explanation that makes sense will typically lend itself to observable outcomes that can be graphed smoothly; and the simpler theory is more likely to eventually be buttressed by an adequate conceptual framework. This is what happened with Torricelli’s hypothesis. The conceptual framework was eventually supplied: the most important causal mechanism behind it is gravity, and, according to the eventually well-established Newtonian laws, gravity’s pull on the air molecules decreases regularly as distance from Earth increases.

16.3.5 Look for Coincidence as an Alternative Explanation

When you cannot think of another explanation, it can be tempting to accept an explanatory argument even when the prior probability of the explanation is exceedingly low. Resist the temptation, especially when you can see that coincidence has not been ruled out as an alternative explanation.

Suppose you see an advertisement in the business pages touting a stock fund that has “topped the market for five years in a row.” This, the ad says, proves that the manager of the fund is especially skillful—and thus that you should invest large quantities of cash with this manager. The leading alternative explanation is that the manager has succeeded by sheer luck. What is the prior probability of this alternative? Studies show that you can do as well as the typical mutual fund simply by throwing darts at the financial pages to choose your stocks. Thus, the prior probability of beating the market in a single year is roughly .50.^[6] The probability of two consecutive years of success is no higher than .50 times .50, or .25. Doing the math for five years, we find that the prior probability of the coincidence explanation is about .03—that is, about 1 in 30 could be expected to have this kind of success just by chance.

And what is the prior probability of the skill explanation? There are a few money managers who succeed on the basis of skill—multibillionaire Warren Buffet is the most famous example. Further, we have a conceptual framework for Buffet’s skill—the causal mechanism makes sense—for his strategies have been widely publicized, and the small handful of others who have had the discipline to follow them have also succeeded over the long run. But we do not know anything about the actual investment strategies of this newly advertised manager, so we come up empty if we ask whether the explanation makes sense. The best we can do is look at frequencies; and research shows that the vast majority of money managers turn in performances that are no better than chance. It is doubtful that more than 1 in 30 is able to win five years in a row on the basis of skill—that is, the probability of succeeding for five years by skill is probably no better than the probability of doing it by chance. In short, coincidence has not been ruled out, so we cannot judge this to be a logically strong argument. Note that I am being careful not to say that coincidence is thus proven to be the correct explanation; the point, a more modest one, is that skill is not supported as the correct explanation. We do not have to establish the correct explanation to establish that the argument is a bad one.

This point is not lost on investment companies. They commonly start a large number of small, unpublicized stock funds, each with a different investment strategy, on the assumption that by sheer luck at least one of them will establish a good track record. The funds that fail are closed, and the manager of the one that succeeds is advertised widely. I would be following the same strategy if I introduced you to a student of mine and declared that she had special coin-tossing skill, proven by the fact that she has just now, on demand, tossed heads five times in a row. You might be impressed until you learn that I asked all 30 students in my class to stand up and try to toss heads. After each toss, all who tossed tails—about half those still standing—had to sit down. There were 15, then 8, then 4, then 2; then, after the fifth toss, this one student remained. The fact remains that she tossed heads, on demand, five times in a row, but you now realize that coincidence is at least as good an explanation as talent—after all, how many people can actually toss heads whenever they want?—and you are likely to lose interest.

This insight can be especially valuable when improbable events are explained by appeal to the paranormal. Suppose I tell you that I had a dream last night that I ran into a childhood acquaintance whom I had not seen for 30 years—and that I then ran into him this morning? Your first thought would probably be that this supports the explanation that we are sometimes able to see into the future via our dreams. But this explanation has an exceedingly low prior probability. No one can even begin to provide an account of the conceptual framework, of the causal mechanisms, that would make sense of it. This is the place to ask about coincidence as an alternative explanation. I have had many thousands of dreams—most of which I have immediately forgotten, in part because they have not come true. By sheer coincidence, a few of these thousands of dreams are going to seem to come true, and these are the ones that will stick most vividly in my memory (remember the vividness shortcut from Chapter 1). Just like the coin-toss and mutual fund cases, coincidence does make sense and is at least as likely here as the paranormal. So the argument’s logic must be considered weak.

16.3.6 Look for Deception as an Alternative Explanation

When an explanation’s prior probability is extremely low, another alternative explanation is deception. My heads-tossing student may have been skillful, or she may have gotten lucky . . . or she may have been secretly using a two-headed coin. Neither of the two alternatives has been ruled out, and either is more probable than that she is one of the very few people who has perfected special coin-tossing skill.

Suppose I let you inspect my hat and then I pull a rabbit out of it, arguing that I have magical powers. That explanation has a nearly nil prior probability, since it does not make any sense; there is no uncontroversial example of this sort of thing actually happening, and we haven’t the slightest notion of the causal mechanisms that would be involved. We do know, however, that deception of this sort happens—that there are entertainers who work very hard at producing illusions like this, and they can make a lot of honest money at it. So, not only is the prior probability of magic negligible, but it is far lower than that of the leading alternative, illusion. The logic of the argument is accordingly weak.

This is not to say dogmatically that magic cannot happen. Rather, it is to say that an argument for magic must meet high standards, and this one does not yet do so. To return to an earlier case, no lesser a light than Thomas Jefferson, when he heard the reports of meteorites from Harvard and Brown professors, said, “I would rather believe that the Yankee professors lied than that stones fall from the heavens.” This was probably reasonable as an initial reaction—though, in this case, the high standards were eventually met.

Nevertheless, smart people suffer lapses of rationality and allow themselves to be persuaded that a man like Uri Geller has special powers because he can perform feats that any practiced illusionist can perform—and can detect. The only difference is that Geller claims that he is not using deception. But this does not make the special-powers explanation more probable than the deception explanation; it simply enlarges the deception.

So-called crop circles in southern England’s grain fields were widely reported in the media a few years ago. These were huge, precise patterns of bent stalks of wheat, corn, and barley that lent themselves to spectacular aerial photographs. Proponents of the paranormal seized on them as new evidence of visitations from other galaxies; said one Patrick Delgado, author of several profitable books on the subject: “No human being could have done this. These crops are laid down in these sensational patterns by an energy that is of a high level of intelligence.” Alas, two British painters finally confessed that they had perpetrated the hoax over a 13-year period simply by pulling around flat, four-foot planks by hand with reins to topple over the stalks. Circles that had only later begun to appear elsewhere, they suggested, were created by copycats. Said author Delgado, “We have been conned. This is a dirty trick. Thousands of lives are going to be wrecked over this.” At least one source of income was going to be wrecked.

Those desperate to discredit a good explanatory argument might misuse this guideline. Just as a good explanatory argument rules out coincidence, it also rules out deception. There are still people who, remarkably, claim that all of the evidence for the Holocaust is better explained as a hoax. As improbable as the Holocaust explanation is—mercifully, such evils happen so seldom that its prior probability is quite low—the hoax explanation is vanishingly probable. Far worse than the plumber explanation from Dear Abby, it requires a long list of independently improbable things all to be true—alternative ways, for example of accounting for the following: the vast documentation rescued from the German Archives; the elaborate sealed rooms set up for funneling the prisoners to their deaths; the movement of enormous quantities of asphyxiating Xyklon B gas to the death camps; the photographs of mounds of bodies; the vast body of eyewitness testimony by both victims and their murderers; and the otherwise mysterious disappearance from history of millions of Jews. The deception explanation should often be considered, but it is subject to the same high standards that apply to any other explanatory argument.

16.4 Summary of Chapter Sixteen

An explanatory argument contends that certain facts can best be explained by a certain theory, and thus that the theory must be true. The first premise states that the theory, or the explanation, really does enable you to predict the facts, or the observable outcome. The second premise states that the observable outcome has happened—that it really has been observed. And the argument concludes that the explanation is thus true. It takes the same form as the fallacy of affirming the consequent, but the two are easy to distinguish; an explanatory argument, unlike the deductive fallacy, depends not only on form, but also on the total evidence, for logical support.

In some explanatory arguments, the explanatory theory is first invented, then the observable outcome is predicted and looked for. In others, the outcome is first observed, then the explanation is invented to account for it; although these are subject to exactly the same evaluative conditions as the first sort, we can more easily be fooled by them. In another type of distinction, some explanatory arguments are general, given that they have application to a wide range of possible observable outcomes; others are singular, in that they apply only to a specific outcome. Again, the two sorts are subject to the same logical standards, though we can shape our inquiry a bit differently in each case.

As with our other inductive arguments, the total evidence condition for logical success has two parts. The first part focuses on the importance of the improbability of the outcome. More precisely, the condition is that the prior probability of the observable outcome must be sufficiently low. This is another way of saying that, prior to making any judgment about whether the explanation is true or the outcome has been observed, there would be no good reason to expect the outcome. If there is good reason to expect it anyway, then the explanation is doing no work and receives no logical support. To test for this, there are several questions that can require “yes” answers. Is the explanation falsifiable? Is the outcome stated precisely? Is there no other explanation of the outcome that already exists? Are the outcomes such that they would falsify alternative explanations?

The second part of the total evidence condition focuses on the probability of the explanation. The explanation’s prior probability—that is, its probability prior to judging whether the observable outcome is true—must not be implausibly low and it must be higher than that of the leading alternative explanations. As with the first part, there are various ways of testing for this. If it is a singular explanation, you can ask if it is the sort of thing that is known to happen, and if it tends to happen more frequently than do the alternatives. For any explanation you can ask whether it makes sense—that is, whether there is an adequate conceptual framework to account for the causal mechanisms required by the explanation. And, finally, you can ask if the explanation is sufficiently simple. In some cases, it can be tempting to accept an explanation with an extremely low prior probability simply because you cannot think of any plausible alternative. In these cases it is better to say that you simply cannot decide, especially if the argument has not ruled out coincidence or deception as alternative explanations.

16.5 Guidelines for Chapter Sixteen

• Structure an explanatory argument, when it would be loyal to do so, as follows: the first premise states that if the explanation is correct, then a specified outcome of it will be observable; the second premise states that the outcome has been observed; and the conclusion states that the explanation is thus correct.
• Be careful not to confuse explanatory arguments with deductive arguments that commit the fallacy of affirming the consequent.
• Be more suspicious of explanatory arguments in which the explanation was invented after the observable outcome was observed.
• As a useful standard, apply the surprise test by asking whether the outcome would surprise you (assuming you reserved judgment about whether the explanation were true and whether the outcome had been observed). If so, then it probably has a low prior probability.
• Reject explanatory arguments that have unfalsifiable explanations; they are in principle unable to satisfy the first part of the total evidence condition.
• Ask whether the outcome is too vague. Vague outcomes are likely to have a high prior probability and thus are likely to signal that the argument is logically weak.
• Ask whether an explanation for the outcome already exists. If an explanation does already exist, then the outcome has a high prior probability and the argument is logically weak.
• Ask whether an outcome rules out the leading alternative explanations. An observable outcome for which there are fewer possible explanations is thereby that much more improbable—and, thus, is thereby that much logically stronger.
• The second part of the total evidence condition for explanatory arguments is this: the probability of the explanation must not be implausibly low and must be higher than that of the leading alternative explanations. This requires imagination in coming up with alternative explanations for the sake of comparison.
• For singular explanations, ask whether this sort of explanation is known to occur and, if so, if it occurs more frequently than do the leading alternative explanations. If the answer is yes, then the argument is at least moderately strong (assuming it has not failed the first part of the total evidence condition).
• For both general and singular explanations, ask whether this sort of explanation makes sense—that is, whether there is a satisfactory conceptual framework for it and whether it is more satisfactory than the alternatives. If the explanation leaves too much to mystery, or requires too much of established science to be replaced by less well-established views, then the argument can normally be no better than logically weak.
• Simplicity contributes to epistemic probability, so ask whether the explanation is sufficiently simple. One test is to ask whether it offers only as many explanatory entities as needed. Another is to ask whether it predicts the smoothest curve.
• If the prior probability of the explanation is extremely low and coincidence has not been ruled out as an alternative explanation, judge the logic of the argument to be weak.
• If the prior probability of the explanation is extremely low and deception has not been ruled out as an alternative explanation, judge the logic of the argument to be weak.

16.6 Glossary for Chapter Sixteen

Confirmation bias—our natural tendency to look for outcomes that support our preferred explanation rather than those that might also falsify the alternatives.

Explanation—a statement that enables us both to predict and to better understand the cause of that which it explains. Also termed a theory or an explanatory hypothesis.

Explanatory argument—an argument whose correct form, assuming that P is the explanation and Q is the observable outcome, is this:

The first premise states that the explanation really does enable you to predict the observable outcome—that it really is an outcome. The second premise states that the observable outcome has happened—that it has been observed. And the argument concludes with the assertion of the explanation. Also called a theoretical argument, inference to the best explanation, hypothetico-deductive argument, transcendental argument, or diagnostic argument.

Falsifiability—the requirement that it be possible to specify some observable outcome of an explanation that could prove it to be false. This is a way of emphasizing the importance of an improbable outcome. To say that an explanation or an outcome is not falsifiable is to say that any observation at all is consistent with the explanation. And it is highly probable that we will have “any observation at all.” So, an unfalsifiable explanation fails the improbable outcome test.

General explanation—an explanation that can apply to a wide range of observable outcomes. Newton’s theories, for example, while applied here to Halley’s comet, actually cover the motion of all objects at all times. General explanations are typical of science, though are not restricted to it.

Observable outcome—what is explained in an explanatory argument; the observable outcome follows from the explanation and can in a certain way, at a certain time, and under certain conditions, be seen, heard, smelled, tasted, or touched. Also termed the data, the prediction, or the facts.

Singular explanation—an explanation that is designed to apply only to a single thing or event. Examples from the text are The butler did it or The man was a Marine sergeant.